| □ R05年12月期 A-10 Code:[HD0306] : 移相(フェーズシフト)形CR発振回路の発振周波数・部品定数等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||
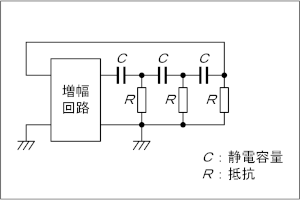 Fig.H3512A10a | |||||||
| |||||||
|
今回(R05年12月期)初出のこの問題、実は一陸技のR02年1月期2回目の「無線工学の基礎」で、A-14等にも出題(これより前にも出題)されていますが、まさか1アマにこのレベルの出題が、と驚くばかりです。一度出たからには、今後も同様の出題が予想されますので、真面目に解説することにします。 なお、一陸技の「無線工学の基礎」の問題には、最近よく出題される「頭の体操」のような抵抗の回路が出題されていたり、参考になるものもありますので、一度目を通しておくこともお勧めします。 [1]ゼロとボーデ線図この問題は「発振回路」の問題なのですが、問題図を見て、何故これが発振するのか、そして「移相型」と呼ばれるのは何故なのか、を考えます。 | |
|
その前に、この回路に特徴的な、コンデンサCと抵抗Rによる「3段のラダー(梯子)回路」について考えます。この梯子の1段について考えると、Fig.HD0306_aの左上のようになりますが、これの「伝達関数」を考えます。もう、「関数」と聞いただけで数学に疎い私などは拒否感が漂いますが、この図にあるように、単に入力電圧Viと出力電圧Voの比です。 細かい複素数の計算は抜きにしますが、伝達関数は交流電源の角周波数をωとして、次のように表せます。 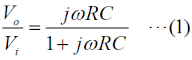 |
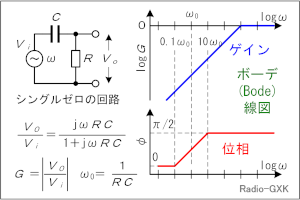 Fig.HD0306_a ゼロのボーデ線図 |
|
「何だ、中身はハイパスフィルタ(HPF)じゃないか」という回路なのですが、伝達関数は(1)式の通り複素数なので、「大きさ(以下、ゲイン)」と「位相」を持っています。この伝達関数の(ゲインと位相の)周波数特性を同時に一つのグラフにしたものが、Fig.HD0306_aの右の図で、このようなグラフを「ボーデ(Bode)線図」といいます(ボード線図、と表記する書物もあります)。 以下、ゲインやRCで決まる角周波数を以下のように定義しておきます。 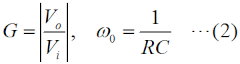 この図を見て分かる通り、Gは周波数に比例して上がりますが、1(=0dB)で頭打ち、位相は0.1ω0あたりの約0度から増加してω0では+45°(=π/4進み)、更に周波数を上げて10ω0でほぼ+90°(=π/2進み)で頭打ちになります。 なお、このような回路を「ゼロ」と呼び、RとCを入替えた回路(LPFになりますが)は「ポール」と呼びます。発振するオペアンプ回路に手を焼いて、発振しないようにするにはどうしたら…と勉強すると出てくる用語です。 また、問題の回路は、ゼロが3段直列になっていますが、3段だけでは位相はトータルで270°(=3π/2)までしか回らないことに注意して下さい。これは、この後の発振条件に関わってきます。 [2]バルクハウゼンの発振条件過去に、トランジスタとLCからなるハートレーとかコルピッツとか(もちろん水晶振動子も)、発振回路にはいろいろ種類があって、回路が発振する条件に関する問題が出題されてきましたが、今回のこの問題は「そもそも回路はどういう条件の時に発振するのか」という根源的な問いも含んでいます。ですので、以下の各内容が理解できると、過去に出題されたこれらの問題も、容易にその解の理由が分かるようになります。何しろ、全ての発振回路は、この条件を満たしているのですから。 | |
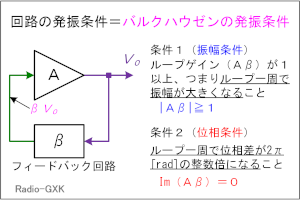 Fig.HD0306_b バルクハウゼンの発振条件 |
Fig,HD0306_bを見ると、フィードバック回路の問題で出てきたのと似たような図が描かれています。ですが、よく見ると、この回路には「入力」がありません。発振回路ですから、入力がないのが普通です。入力はありませんが、出力の一部を「帰還」しているので、発振回路はフィードバック回路の一種です。どんな帰還でもいいわけではなく、発振回路のとなるには、その「帰還のかけ方」にカギがあります。 そのカギというのが、バルクハウゼンの発振条件と呼ばれるものです。 まず、図の増幅器の利得をA、フィードバック回路の帰還率をβとします。両者とも、周波数の関数で、かつ、位相も含む複素数であることに注意して下さい。 バルクハウゼンの発振条件は、次の2条件からなっています。 |
|
【条件1】 振幅条件 発振周波数におけるループゲインの大きさが1以上(つまり1≦|Aβ|)であること。言い換えると、このフィードバックループを一周すると、信号の振幅が大きくなっている、ということを意味します。実際の発振回路では、無限に大きな振幅の出力が得られるわけではなく、回路利得が飽和して、一定の振幅に漸近します。 【条件2】 周波数条件 ループを一周すると、元の信号との位相差が2π [rad]の整数倍(±2π、±4π…)となること。数学的に言えば、複素数Aβの虚数部がゼロ、つまり、Im(Aβ)=0です。フィードバック回路で言うと、これが正帰還が掛かっている状態になります。また、普通の発振回路では、位相差は2πです。 帰還(フィードバック)回路に位相をシフト(移相)させる働きを持たせ、増幅器と合わせてバルクハウゼンの発振条件を満たす、という発振回路だから「移相形」という名前になった、というわけです。 少し余計なことを書いておくと、実は発振が開始するために、上の2条件だけでは不足です。この回路は入力がないので、発振が始まるためには「種」が必要です。通常は、電源を入れた際のノイズ等に発振周波数の成分が入っていて、これが増幅されてループを何周もするうちに飽和し、定常状態に至ります。 この回路は発振回路なので、意図して発振を起こしているわけですが、「意図しない発振」であっても、このバルクハウゼンの発振条件は満たされて起きるので、高周波の場合、結合を生む回路や配線間の浮遊容量・浮遊インダクタンスを減らすように、距離を離したりシールドするなどして(主に)振幅条件を満たさなくする対策をします。 [3]増幅回路は負帰還か正帰還か問題図には「増幅回路」という箱が描かれているだけで、この増幅回路がどういう性質なのか全く分かりません。特に、位相に関して入力に対するズレ(正帰還の0 [rad]か、負帰還のπ [rad]か)が分からないと、周波数条件が決められません。ただ、よく考えると、Fig.HD0306_aで見たように、フィードバック回路では最大でも3π/2しか位相がズレないので、もしこの増幅回路が正帰還であれば、位相ずれを足しても2πにならず、周波数条件が満たされないことが分かります。一方、負帰還であれば、増幅回路でπ [rad]に加え、帰還回路でπ [rad](3段でπ/3 [rad]ずつ)を分担すれば、ループ一周で2πとなり、発振条件が満たされます。 なお、詳しい計算によれば、3段のゼロの各段の位相シフトは、正確にπ [rad]の3等分ではなく、微妙にπ/3 [rad]からズレているそうです(自分で計算したわけではないので)。 [4]あとはひたすら計算この回路について、同じ回路(ゼロ)が3段直列なのだから、何かエレガントな解法があるのでは、と考えてみましたが、私の頭では無理なようなので、愚直に回路方程式を立てて解き、最後にバルクハウゼンの発振条件を適用します。 | |
|
まず、フィードバック部分の3つの回路ループについて、キルヒホッフの閉路方程式を立てて行きます。 つまり、Fig.HD0306_cのフィードバック部分の3つのループについて、左からi1、i2、i3 の方向に電流を考え、各ループ内の電圧降下の和がゼロ、という方程式を立てます。 なお、増幅回路の入力電圧をvi 、入力インピーダンスは∞、出力電圧をvo 、出力インピーダンスはゼロとします。図から分かるように、vi は一番右の抵抗の両端の電圧に等しくなります。つまり、 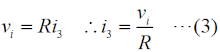 です。 |
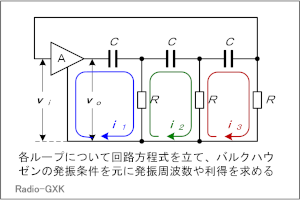 Fig.HD0306_c 回路方程式の立て方 |
この図の左からループ1〜3について、閉路の方程式は、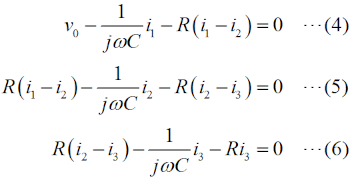 と立てられます(同様のキルヒホッフの法則を使ってループ内の電圧に関する方程式を立てて解く問題はH1104A05等を参照して下さい)。 (4)〜(6)式を電流×抵抗、という項に整理します。 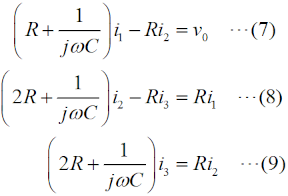 このうち、(7)式をi1 について解いて、 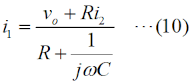 と求めます。(10)式で求めたi1 を(8)式に代入すると、 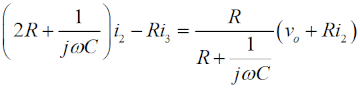 となりますが、この式の両辺をRで割って、 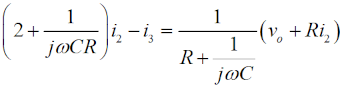 とします。さらに、両辺に[R+(jωC)-1]をかけて、 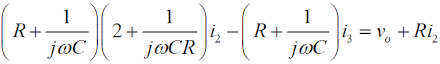 と求めて左辺第一項のカッコをばらし、左辺=voという形にすれば、 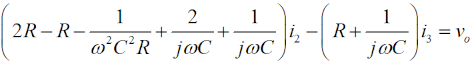 となります。さらに整理して、 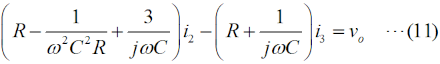 と求めます。ここで、(9)式をi2 について解けば、 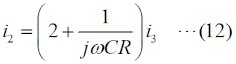 となりますので、これを(11)式のi2 に代入して、 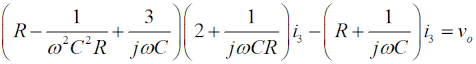 上記の左辺を全部一度カッコを外してバラバラにして整理(単純計算なので省略しますが)すれば、 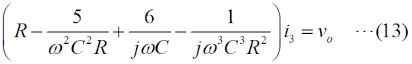 となります。ここで、(3)式のi3 を(13)式に代入して、左辺を実数部と虚数部に分けて整理すれば、 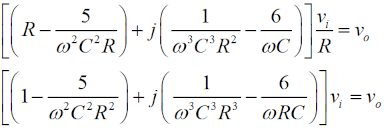 となります。さてここで、この式を眺めてみると、左辺にvi のかかった項、右辺はvo ですから、増幅回路の利得Aはこの式の両辺をvi で割ればよく、 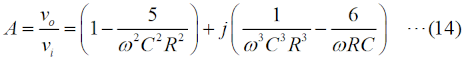 と求められます。バルクハウゼンの発振条件のうち、周波数条件はこのフィードバック系の虚数部がゼロと言っているので、次が成り立ちます。 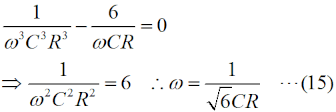 これが、この回路の発振(角)周波数です(周波数を求められている時は、2πで割るのを忘れずに)。さらに、増幅器の利得Aは、この(15)式を(14)式に代入して、 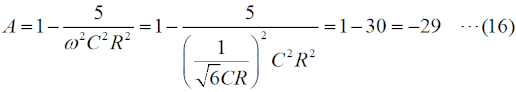 と求められます。つまり、増幅器は反転増幅(なので負号がついている)で、その大きさは29あれば、角周波数ωで発振が持続する、ということです。 仮に、利得の大きさが29を超えていても、利得が飽和してこの周波数で発振します。 それでは、解答に移ります。 まず、単位に注意して下さい。求められているのはkHz単位の周波数で、角周波数ではありません。(15)式の右辺を2πで割って、C、Rに各々0.01 [μF]、5 [kΩ]を代入すれば、求める周波数は、 f=1/[2π(√6)×0.01×10-6×5000]=10000/(π√6) [Hz]=10/(π√6) [kHz] となります。従って、解答は1と分かります。 解説のような複素数計算を、試験時間中に行うことは無理でしょうから、解答は覚えておくしかありません。また、冒頭に述べましたように、この問題は一陸技の「無線工学の基礎」に出題されている問題と同類(設問の内容が異なる)です。一陸技の方には、この移相型発振回路の動作の特徴や増幅回路に必要な利得等が正誤問題としても出ています。全く同じ問題が出るとは限りませんが、計算問題以外も出題される可能性があるので、見ておいた方が良いでしょう。 | |
 |
 |