□ H24年12月期 A-10  Code:[HD0403] : 移相法によるSSB変調器の構造と原理、フィルタ法との比較
検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます  ■ 無線工学を学ぶ  (1) 無線工学の基礎   年度別出題一覧   H11年 4月期,8月期,12月期   H12年 4月期,8月期,12月期   H13年 4月期,8月期,12月期   H14年 4月期,8月期,12月期   H15年 4月期,8月期,12月期   H16年 4月期,8月期,12月期   H17年 4月期,8月期,12月期   H18年 4月期,8月期,12月期   H19年 4月期,8月期,12月期   H20年 4月期,8月期,12月期   H21年 4月期,8月期,12月期   H22年 4月期,8月期,12月期   H23年 4月期,8月期,12月期   H24年 4月期,8月期,12月期   H25年 4月期,8月期,12月期   H26年 4月期,8月期,12月期   H27年 4月期,8月期,12月期   H28年 4月期,8月期,12月期   H29年 4月期,8月期,12月期   H30年 4月期,8月期,12月期   R01年 4月期,8月期,12月期   R02年 4月期,9月期,12月期   R03年 4月期,9月期,12月期   R04年 4月期,8月期,12月期  分野別出題一覧   A 電気物理, B 電気回路   C 能動素子, D 電子回路   E 送信機, F 受信機   G 電源, H アンテナ&給電線   I 電波伝搬, J 計測  ■ サイトポリシー  ■ サイトマップ[1ama]  ■ リンクと資料  ■ メールは下記まで 2022年 12/31 12月期問題頁掲載 09/01 08月期問題頁掲載 05/14 04月期問題頁掲載	無線工学 > １アマ > H24年12月期 > A-10 A-10 次の記述は、ＳＳＢ（Ｊ３Ｅ）波の発生方法について述べたものである。［　］内に入れるべき字句の正しい組合せを下の番号から選べ。 (1) フィルタ法では、まず、平衡変調器やリング変調器を用いて、［Ａ］を発生させ、次に、いずれか一方の側波帯のみを取り出す。 (2) 図は、移相法によるＳＳＢ変調器の構成例を示したものである。この方法は、フィルタ法に必要な急峻な［Ｂ］が不要な反面、信号波の全域にわたり平坦な位相特性を有するπ/2移相器が必要である。デジタル信号処理の発展に伴うデジタル移相器の実現により、この方法が実用化されている。 Fig.H2412A10a Ａ Ｂ １ 抑圧搬送波両側波帯 帯域フィルタ（ＢＰＦ） ２ 抑圧搬送波両側波帯 帯域除去フィルタ（ＢＥＦ） ３ 低減搬送波単側波帯 帯域フィルタ（ＢＰＦ） ４ 低減搬送波単側波帯 帯域除去フィルタ（ＢＥＦ）
	久々の、歯ごたえのある新問です。この問題で問われているのは、１アマでは私が記憶する限り初めての出題となる、移相法によるSSB波の発生法です。「移相法って何だ？」という方も多いと思いますので、原理から説き起こします。そのため、どうしても数式が多くなりますが、高校の理系コース程度のレベルです。数式を用いれば、フィルタ無しで片側の側波帯だけが取り出せる原理が、鮮やかに表現できます。 　もし、数式が理解できなくても、問題で問われていることは計算ではないので、移相法の特徴を暗記しておけば解けるでしょう。 ［１］移相器の働き 　まず、移相法のキーとなる、移相器について簡単に調べておきます。 Fig.HD0403_a π/2位相器の動作 　移相器は、入力の交流の位相を、一定の位相角だけ遅らせる、又は進めるものです。通常よく用いられるのは、π/2だけ進めたり遅らせたりする位相器です。この解説では、「遅れ」の方を採用しますが、ＳＳＢ波を得る目的では、どちらを使っても同じです。 　π/2だけ位相を遅らせる、ということは、入力がcos波ならsin波が、入力がsin波ならcos波が出力される、ということです。 　このことは、下記の三角関数の公式から得られる結果です。例えばcosの三角関数のグラフを書いて、π/2だけ前後にずらすと、sinや-sinのグラフに重なる、というあれです。 　 　このような回路を設計しようと単純に考えれば、入力に一定時間の遅延を加えてやれば、位相が遅れて出てくるので、簡単なように思います。しかし実際には、搬送波は必ずしもいつも同じ周波数ではありませんし、信号波（被変調波）の場合は音声等の、いろいろな周波数成分の重ね合せで表現される波ですから、考えている帯域内のいかなる周波数に対しても、一定の移相量となる特性を持たせるのは、簡単でないことは想像できます。 　これには、最近のデジタル信号処理技術を応用することで解決策があるのですが、それはこの解説の最後の方で。 ［２］平衡変調器の動作 　次に、平衡変調器の動作を復習しておきます。これは、過去にもいくつか類題が出題されていますので、詳細は、例えばH2004A09等の解説を参照して下さい。 　平衡変調器は、信号波と搬送波を入力してやると、上下の側波帯（サイドバンド）のみが出力される回路で、通常は搬送波は出力されません。平衡変調器の中身は、大概が半導体素子の非線形現象を用いた乗算器です。 　乗算器で、なぜ上下の側波帯が出てくるのかは、再び三角関数の公式のお世話になります。ここで使うのは、(3)から(5)式のいわゆる「積和の公式（積を和に直す公式）」です。 　これらの式の右辺を見ると、２つの入力のsinとcosがどのような組合せであっても、αとβ（α≠β）の和と差の成分が見えています。搬送波を中心に上下の側波帯のみが出力される、ということがこの式から分かります。 Fig.HD0403_b 平衡変調器の動作 　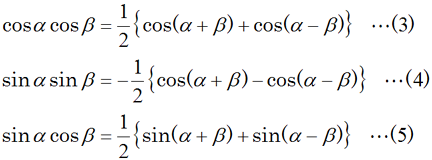 　より具体的に、搬送波をＶC＝ＥCcosωCt [V]、信号波をＶS＝ＥScosωSt [V]とします。これらの積を取れば、平衡変調器の出力ＶOC [V]は、 　 ここに、ＥO＝ｋＥCＥSです。ｋは平衡変調器の変換利得です。(6)式では搬送波、信号波ともにcosでしたが、この後の計算のために両方-sin、つまり、搬送波をＶC＝-ＥCsinωCt [V]、信号波をＶS＝-ＥSsinωSt [V]とすると、平衡変調器の出力ＶOS [V]は、 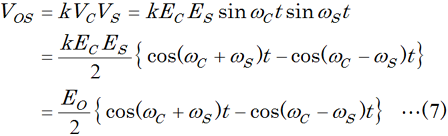　 という信号が得られます。 ［３］移相法でＳＳＢ波を得る原理 　ここまでは、移相法の構成要素とその動作について説明してきました。上の(6)及び(7)式を見ると、もう答えが見えている方もおられるかも知れませんが、平衡変調器とπ/2移相器を使ってＳＳＢ波を得る構成と原理を見て行きます。 Fig.HD0403_c 移相法ＳＳＢ変調器の原理 　移相法を用いたＳＳＢ変調器のごくシンプルなブロック図をFig.HD0403_cに示します。 　信号波は、2本に枝分かれして、一方にのみπ/2移相器が接続されています。搬送波も同様です。 　この構成では、信号波、搬送波共に移相器を通らなかった枝、移相器を通った枝が各々平衡変調器に入力されます。つまり、信号波、搬送波共にcosであるとすると、移相器を介しない平衡変調器１には信号波のＥScosωStと搬送波のＥCcosωCtが入力され、他方、平衡変調器２には信号波の-ＥSsinωStと搬送波の-ＥCsinωCtが入力されることになります。 　そこで、(6)式で示される平衡変調器１の出力ＶOCと、(7)式で示される平衡変調器２の出力ＶOSとを加算すれば、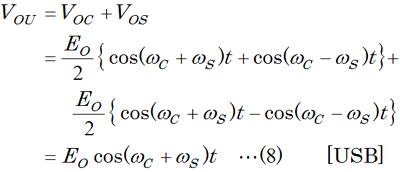 　 となって、上側側波帯（ＵＳＢ）が得られます。下側側波帯（ＬＳＢ）を得るには、加算ではなく減算（回路的には、反転して加算）すればよく、 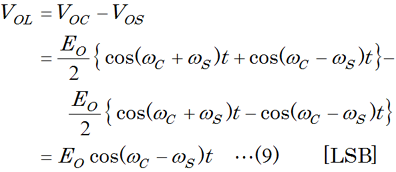　 となります。 　ここまでの説明では、「数式がこうだからこういう信号が得られる」式になっていて、数学ありきになっていて面白くないのですが、物理としては、π/2位相をずらした信号で平衡変調を掛けると、ずらさないで平衡変調を掛けた出力と比べて片側の側帯波成分の符号が違う、という特性を利用しています。ですから、上の例で言えば、加算すればＬＳＢ成分が相殺してＵＳＢが、減算すればＵＳＢ成分が相殺してＬＳＢが得られる、ということになります。 　音声信号で変調を掛ける場合、平衡変調器等を使った方法では、出力に両側波帯が出てくるので、変調器の後段に音声帯域のかなりシャープなバンドパスフィルタがないと、不要な側帯波の減衰量が十分確保できないという問題のため、技術的にハードルが高いです。この方法なら（帯域内でフラットな移相特性を持つ移相器をどう実現するか、という別な困難はありますが）フィルタに関する課題を克服する必要はありません。 ［４］デジタル技術が支える変調技術 　我々アマチュアが使う無線機の中にも、ＤＳＰ（Digital Signal Processor）という、信号処理に特化した高速演算器（ＤＳＰについてはH2404A15を参照下さい）が搭載されたものが出てきています。搬送波はアマチュアでＨＦから50MHzと考えると、ＤＳＰの内部クロックはそれをはるかに上回るGHzオーダーのものもあります。 　１クロックで積和（乗算＋加減算）が行なえるＤＳＰを使えば、ＨＦと50の無線機なら、ここに書いた移相器や平衡変調器を、デジタル的に構成することができます。信号波はもちろんのこと、搬送波までデジタル値として、乗算や加減算を全部デジタル的にやってしまおう、ということです。 　こうなってくると、上に書いたような、帯域内で全域にわたるフラットな移相・位相特性を持った移相器や高次のひずみが原理上生じない変調器を構成することが可能になります。プログラムで制御しますから、アナログ回路特有の部品のバラツキを考慮する必要もありません。（とはいえ、誰でも作れるほど簡単ではなく、内部の演算はスピード確保と誤差をどう少なくするか、というノウハウの塊なのですが…） それでは、解答に移ります。 　平衡変調器やリング変調器が出力するのは、ＡＭ変調（Ａ３Ｅ）波から搬送波を取り去ったもの、つまり抑圧搬送波両側波帯です。この信号から、上下どちらかの単側波帯を取り出すには、シャープなスカート特性を持った帯域フィルタ（ＢＰＦ）が必要ですが、位相法には、ブロック図を見ての通り、これが必要ありません。 　従って、正解は１と分かります。
閉じる