| □ R06年12月期 A-24 Code:[HE0306] : 単一正弦波で変調したAM波のスペクトル振幅から変調度を求める |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||
| |||||||||||||||
この問題は、今回(R6年12月期)が初出ですが、昔はスペアナを使って変調パラメータを測定する、というのはプロの世界の話でした。今や、ポータブルで安価でも数GHzまで測れる物も出てきているので、今後も「スペアナで変調パラメータを測る」問題は増えると思います。[1]振幅に着目…数学が得意な方向けこの問題は、解き方が(少なくとも)2つあります。最初は、数学が得意な方、三角関数の公式等をきちんとマスターされた方向けです。なお、この解説を通して、振幅変調波の変調波は単一周波数の正弦波であることを前提とします。三角関数の積を和に変える公式は、 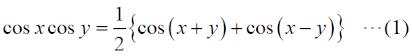 です。搬送波や信号波の式で、cosとsinが入れ替わっている場合もありますから、左辺のsinやcosが入れ替わっている公式も同様に記憶しておく必要があります。ただ、sinがcosに変わったり、その逆があっても、搬送波や信号波の位相がπ/2ズレるだけで、以下の振幅や電力の議論の本質に差はないので、ここではこの一つの公式だけを挙げておきます。 ここで、搬送波の(角)周波数をωc [rad/s]、信号(被変調)波の(角)周波数をωp [rad/s]、搬送波の振幅をV [V]、変調度をm、時間をt [s]とすると、振幅変調波の信号e [V]は以下の式で表されます。 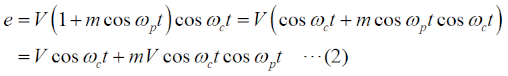 (2)式の第二項、を、(1)式を使って書けば、 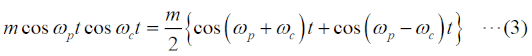 となりますから、(2)式をさらに詳しく書けば、 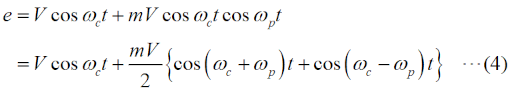 となります。(4)式の右辺第一項(cosωctの項)は搬送波、右辺第二項(mV/2がかかっている項)の{ }の中が(ωc+ωp)の上側波帯(USB)と(ωc−ωp)の下側波帯(LSB)になります。つまり、この(4)式が、スペアナの画面に現れる搬送波と両側波帯の信号波形を表しているのです。 USBとLSBの成分の振幅は同じなので、各々の振幅成分(搬送波の振幅:VCar、片側の側帯波の振幅:VSSB)だけを抜出して関係を書けば、 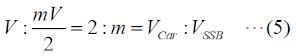 となります。後は、問題で問われている(求めるべき)パラメータに応じてこの比例式を解いて、 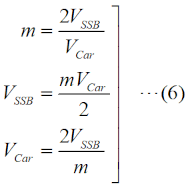 のいずれかを求めれば良いわけです。 [2]電力に着目…比だけで解ける | |
|
上の解き方は、三角関数の公式((1)式)を正確に記憶している必要がありますが、私などはcosとsinが入り乱れて、正確に記憶できません。ここでの解き方は、そのような方向けですが、振幅変調波の搬送波と側帯波成分の各々の電力についての関係式(下記(7)式)だけは記憶している必要があります。これを理解していれば、後は比の計算だけで解けます。 そのカギは、電力∝電圧2であることです。もちろん、交流回路においては、比較する2種類の電圧が同じインピーダンスの回路のものである必要がありますが、高周波の計測系は通常50 [Ω]に統一されていますので、電力∝電圧2が成り立ちます。 |
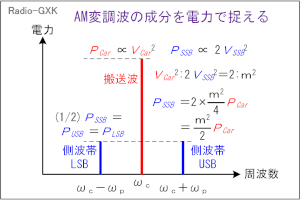 Fig.HE0306_a AM変調波のスペクトルと電力 |
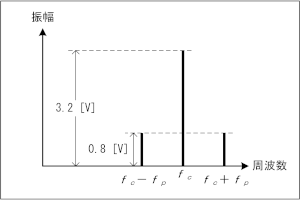
搬送波の電力をPCar [W]、両側帯波の合計電力をPSSB [W]とすると、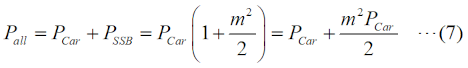 が成り立ちます。なお、この式自体が問題になっているものの解説は、H2008A13等を参照して下さい。 この式が言っているのは、搬送波電力を1とすると、両側帯波の電力(の合計)はm2/2(片側の側帯波では半分のm2/4)だということです。ここで、搬送波振幅をVCar、片方の側波帯の振幅をVSSBとすれば、上で述べた電力∝電圧2の関係を使って、 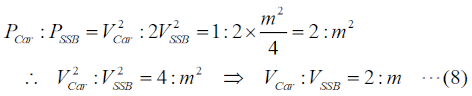 ということです。(8)式から問題で問われている(求めるべき)パラメータに応じてこの式を解いて、 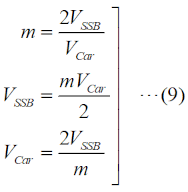 となりますが、これは当然のことながら(6)式と一致します。 それでは、解答に移ります。 題意の数値(VCar=3.2 [V]、VSSB=0.8 [V])を(6)式又は(9)式の一番上の式に入れれば、m=0.5(50 [%])と求められます。従って、解答は4と分かります。 問題文にもありますが、グラフの縦軸はリニア(比例)軸になっています。通常は、スペアナの縦軸は[dB]なので、問題を解きやすくしてくれている、とも考えられますが、dB表記のままでも解けるようにして下さい(「現場」ではその方が役に立ちます)。 | |
 |
 |