| □ R06年12月期 A-02 Code:[HA0705] : 環状の磁芯に巻いたコイルのインダクタンスと巻数、断面積、透磁率等の関係 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
これまで、コイルに電流を流して磁界を作り、その磁界を磁性体で「束ね」た結果の磁束密度を求める問題は、出ていません。ただ、磁界と磁力線、磁束密度等の概念は知識としてある程度ある、という前提で、以下の説明をいたします。[1]起磁力・磁気抵抗・磁束の関係以下、電流は直流で考えます。コイルに電流を流すとコイルの周りに磁界ができます。コイルを(空芯や樹脂ではなく)磁性体に巻くと、磁力線が集められ、磁束密度が上がります。ここでは、磁性体をトロイダルコアと考えて、これに巻いたコイルの巻数や流す電流、コアの形状、磁性体の透磁率等の関係を定量的に見て行きます。 まず、Fig.HA0705_a左のようなトロイダルコアがあるとします。コアの断面は長方形で、内径がa [m],外径がb [m]、厚みがt [m]とします。これに、コイルをN回巻いて、電流をI [A]流すと、磁束φ [Wb]や磁束密度B [Wb/m](単位はテスラ [T]でも同じです)はいくらになるか、ということを考えます。 磁力線の平均磁路長l [m]は、 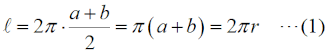 で求められます。これは幾何学的な話なので、特に解説は不要と思います。コアの断面積S [m2]は、 | |
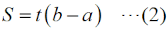 これも特に説明は不要かと思います。厚みがt、幅がb−aの四角形(コアの断面)の面積です。磁束φ [Wb]は、 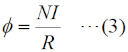 です。NIを「起磁力」(磁力線を発生させようとする「力」)、Rは「磁気抵抗」と呼びます。この名前から想像されるように、起磁力=起電力、磁気抵抗=抵抗、と考えると、(3)式はオームの法則で電流を求める式に該当します。 |
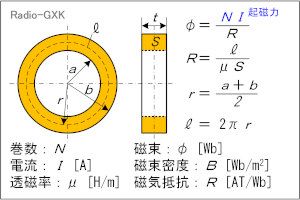 Fig.HA0705_a トロイダルコアの磁束計算 |
ここで、磁気抵抗R [AT/wb](ATは「アンペアターン」と読みますが、電流×コイルの巻数のことなので、単位は電流{A]と同じです)についても考えておきます。磁気の場合、物質の透磁率μ [A/m]が大きいほど、反比例して磁気抵抗Rが小さくなります。つまり、磁力線はその物質を「通りやすく」なります。また、電流と同様、磁力線が通る方向に垂直な断面積が大きいほど、反比例して磁気抵抗Rが小さくなります。抵抗と同じで、磁力線が通る長さlに比例して、磁気抵抗Rは大きくなります。このことをまとめれば、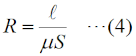 となります。 ここまでは、単純にコアの性質(透磁率)と形状、電流と巻数から、磁気抵抗や磁束を求める方法を述べました。 [2]磁束密度や透磁率はどうなるか次に、磁束密度B [Wb/m2]や透磁率μを求める式を導出しておきます。まず、磁束密度ですが、磁力線が通る物質の面積Sに一様に磁力線が分布するとすると、磁束密度は磁束φを断面積Sで割ればよいので、(1)式、(3)式、(4)式を使って、 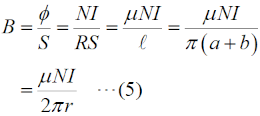 と求められます。この式でちょっと不思議なのは、断面を通る磁力線の密度が磁束密度Bにもかかわらず、断面積Sが消えて不要になっていることです。透磁率μは(5)式をμについて解いて、 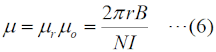 となります。ここで、μ0は真空中の透磁率(=4π×10-7 [H/m])です。もし、透磁率μではなく、比透磁率μrで問われたら、 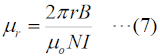 で求めることができます。 その他にも、問題として、磁束密度が分かっていて電流や巻き数を求める問題等が出ても、これらの式を変形すれば求められるでしょう。 それでは、解答に移ります。 この問題が問うているのは、比透磁率μrです。(7)式から求められるので、N=250、I=1 [A]、r=4×10-2 [m]、B=5 [T]([Wb/m μr=4,000 と求められます。従って、解答は4と分かります。 | |
 |
 |