| □ R06年04月期 A-20 Code:[HH0308] : シュペルトップ(バズーカ)の平衡−不平衡変換の原理と構造 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||||||||||||
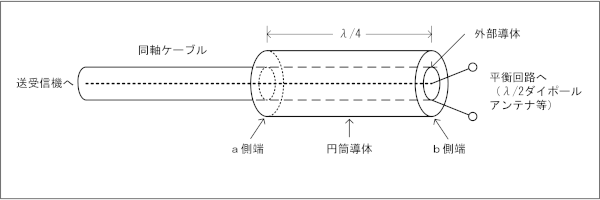 Fig.H3604A20a | |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||
この問題は、今回(R6年4月期)初出ですが、今後も出題されることが予想されます。高周波電流にとって、大きな意味を持つλ/2やλ/4という長さを応用して、いろいろな回路が作れる、好例だからです。[1]バズーカ(シュペルトップ)とはアマチュアの使うアンテナは、ダイポールや八木等、平衡型の物が多いですが、リグからアンテナ迄のケーブルは、不平衡型の同軸ケーブルが殆どです。平衡負荷と不平衡線路(同軸ケーブル)を直接繋いでしまうと、同軸ケーブルの外側導体の外側に漏洩電流(地電流)が流れるので、この電流を流れないようにしなければなりません。その働きを担うものがバランです(漏洩電流が流れる理由や、一般的なバランの効果については、H1208A21の[4]等を参照して下さい。ここでは、この内容は知識としてあることを前提に説明します。 | |
|
バズーカバランやシュペルトップ(Shperrtopf)と呼ばれるものは、バランの一種です。構造は、Fig.HH0308_a左上の断面図のようなもので、同軸ケーブルの上から(ここでは)円筒導体という金属の「さや」を被せ、それを無線機側の端点で同軸の外側導体に接触させたものです。円筒導体のアンテナ側はオープン(開放)にします。円筒導体の長さ(電気長)はλ/4とします。波長が関係してきますから、広帯域バランではありません。アマチュアの場合なら、決まったバンドのアンテナにしか効果がありません。 同軸と円筒導体が重なっている部分の断面を拡大したのが、Fig.HH0308_aの下の絵になります。 |
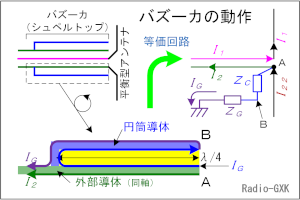 Fig.HH0308_a バズーカの動作原理 |
|
さらに、これを高周波的に等価回路で描いたのが、Fig.HH0308_aの右上になります。 平衡型アンテナの(この図で)上側と下側のエレメントに流れる電流は、本来大きさが等しくなければなりませんが、ここではアンバランスになっていると仮定して、上側エレメントにI1が、下側エレメントにI22の大きさの電流(I1≠I22)がそれぞれ流れているものとします。 上側のエレメントは同軸の芯線に直結なので、同軸の芯線に流れる電流もI1になりますが、下側のエレメントはそうはいきません。下側のエレメントの電流I22は、図のA点で分岐して、一方は外導体の内側を流れる電流I2となり、もう一方は漏洩電流IGとなります。 [2]高周波電流の流れ方ここで、「(Fig.HH0308_aの下のように)同じ導体の裏と表で流れる電流が違うなんてあり得るのか」という疑問が湧きます。また、仮にそうだとしても「表の電流と裏の電流は、どう区別する(流れる経路がどう決まる)のか」という疑問もわきます。実は、これが高周波の面白い所で、これが分かると高周波回路、プリント基板の設計が、一気に高度になります。 | |
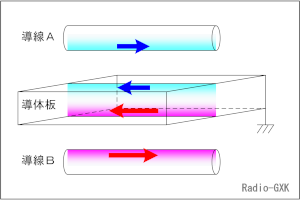 Fig.HH0308_b 高周波電流の流れ方 |
まず、高周波では表皮効果(H1312B01)が顕著で、HF帯以上の周波数の電流は導体の表層の数 [μm]〜数10 [μm]程度の所しか流れていません。厚みのある導体であれば、表と裏で異なる電流が流れることも、高周波では何らの不思議もありません。 次に、電流の流れる面はどう決まるのか、ですが、Fig.HH0308_bのように広い面積の導体板の直上と直下に、導線AとBがあり、それぞれ大きさの違う高周波電流が流れているとします。この時、導体坂の導線Aに近い側の面には導線Aの「戻り電流」が、導線Bに近い側の面には導線Bの「戻り電流」が、それぞれ流れます。 |
つまり、導体坂に流れる電流の面は、それと対になる逆向きの電流に近い面上を流れる、ということです。導体坂と導線の間の狭い空間には電磁界ができていますが、往きと還りの電流が互いを引き寄せるように、電流の経路・面が決まるのです。[3]漏洩電流をゼロにする再び、Fig.HH0308_aに戻ります。この図の等価回路の、下側エレメントを流れる電流I22については、次が成り立ちます。I22=I2+IG ∴ IG=I22−I2 …(1) ここで、我々が目指すのは、IG=0の状態です。一方、同軸ケーブルというのは、芯線を流れる電流と外側導体の内面に流れる電流の大きさが同じで向きが逆、つまり、 I1=I2 …(2) です(大きさを比較しているので負号は付かない)。漏洩電流IG=0になれば、(1)式から I22=I2 …(3) となります。(2)式と合わせて、 I1=I22 …(4) の状態、つまり平衡型アンテナの両側のエレメントに大きさが同じ電流が流れる状態を作ることができます。ここまではまあ、当たり前と言えば当たり前の結果ですが、問題は、どうやってIG=0の状態を作り出すか、です。 [4]ZCを∞にする…同軸トラップがヒントIG=0にするには、Fig.HH0308_aの等価回路の図で、ZGかZCのどちらかを∞にすればよいのですが、そもそもZGはアンテナと大地の間にある結合を意味していますので、アンテナを無限遠の宇宙空間に持って行くなどしない限り∞にはできません。となると、ZC=∞にすればよいことになりますが、これにはどうすれば良いでしょうか。ヒントはH3304A20の同軸トラップです。同軸トラップでは、基本波に当たる周波数で、λ/4波長になるような先端が短絡の伝送線路を組めば、トラップの根元から見たインピーダンスが∞になるので、基本波は影響を受けません。ところが、2倍高調波の周波数から見るとインピーダンスが0になるため、トラップとして動作します。 [5]金属円筒が漏洩電流に対して持つインピーダンスを計算するここで、Fig.HH0308_a下の図をA−Bを端とする伝送線路として見てみると、先端(同軸の外側導体と金属円筒の短絡接続点)までの長さはλ/4ですから、同軸トラップの解説の式(1)のβdが(2π/λ)×(λ/4)=π/2と計算できます。これをこの解説の(1)式に代入(この式で tanβd=∞、Z0≠0、ZL=0)すれば、Z=∞と求められます。つまり、漏洩電流から見た、円筒導体を同軸ケーブルに挿入した部分のインピーダンスZC=∞となり、上で述べたような、IG=0が実現するわけです。なお、ここでいうλは、自由空間中の波長ではなく、Fig.HH0308_aの黄色の部分の絶縁物が間に入った伝送線路上の波長であることに注意して下さい。このバランを自作する際、黄色の部分は同軸のシースを流用することが多いですが、塩化ビニル等の樹脂だとすると、比誘電率が3〜5程度ありますので、λを自由空間中の波長λ0で計算してしまうと、λ/λ0=0.45〜0.58となり、バズーカは殆どバランとして動作しません。 また、同軸の外側導体(通常は編組線)と金属円筒の接続点では、円周方向にわたって全周をきっちり接触させる必要があります。これを怠ると、同軸の編組線に漏洩電流が漏れてしまいます。 [6]応用範囲が広いλ/4長の導体スリーブアンテナのスリーブ(H1212B04)やグランドプレーンアンテナの地線(ラジアル)等、高周波ではこのλ/4のインピーダンス特性を利用したものが数多くあります。これらは、λ/4のラインがインピーダンス=∞の性質を持つことを利用して、この周波数の電流を不要な部分(例えば同軸カーブルの外側導体の外側)に流さない働きをしています。 それでは解答に移ります。 A…金属円筒と同軸の外側導体の接触点は、問題図のa端側に置きます B…円筒導体の開放端側(b点)で、インピーダンスが非常に大きくなります C…不平衡回路と平衡回路を直接接続して生ずるのは不平衡電流です となりますから、解答は2と分かります。 | |
 |
 |