| □ R05年12月期 A-08 Code:[HD0110] : ダーリントン接続の、構成と動作原理、特性の説明 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||||||||
|
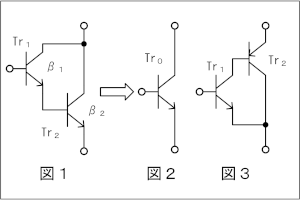
図1の原理的構成例に示すように、トランジスタTr1及びTr2をダーリントン接続したとき、図2に示すように等価的に一つのトランジスタTr0とみなすことができ、Tr0のエミッタ接地直流電流増幅率は[A]で表される。 図1の接続では、Tr1のエミッタ電流がTr2のベース電流となるので、Tr1はTr2に比べて一般に小電力用トランジスタが使用できるとともに、Tr1の入力インピーダンスがTr2の入力インピーダンスの[B]倍として作用するので、入力インピーダンスが非常に大きくなるという特徴がある。 図3に示す構成例もダーリントン接続であり、この場合は等価的に一つの[C]トランジスタとみなすことができる。 | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
複数トランジスタを「直接」接続した回路は、今回(R05年12月期)初めて出題されました。通常の増幅回路では、1段目の増幅、2段目の増幅、というように各段で独立した設計になっており、段間はなるべく干渉が起きない(繋がっている相手の影響受けない)ように設計しますが、この問題のように直接トランジスタ同士を接続することで、あたかも一つのトランジスタのように扱います。[1]バイポーラトランジスタのダーリントン接続とはバイポーラトランジスタのダーリントン接続とは、通常2個のトランジスタを用い、Fig.HD0110_a左のように接続した回路です。 | |
|
Q1とQ2はバイポーラトランジスタですが、この後に述べるように、この回路を使うのは電流増幅度を大きく取りたい場合なので、Q1は小信号トランジスタでもQ2はパワートランジスタ、ということが多いです。 ここで、解析のための変数を定義します。 まず、Q1について、ベース電流、コレクタ電流、エミッタ電流、電流増幅率(直流でも交流でも)をそれぞれIB1、IC1、IE1、β1、とします。 次に、Q2も同様にIB2、IC2、IE2、β2とします。 なお、各トランジスタは飽和したりすることなく、ほぼ線形に動作する領域で解析するものとします。 |
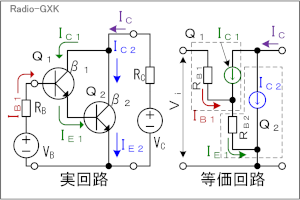 Fig.HD0110_a ダーリントン接続のモデル化 |
これ以降では、バイポーラトランジスタの回路モデルとしての動作を理解している必要があります。これについての解説は、H1104A11等をご参照下さい。[2]ダーリントン接続の解析 その1…電流増幅率Fig.HD0110_aの右の回路は、左の実回路を簡単にモデル化したものです。RB1やRB2というのは、ベースから見た等価的な入力抵抗です。また、ICはダーリントン接続を「一つのトランジスタ」と考えた時のコレクタ電流、Viはベース入力の電圧です。以下、この回路モデルで考察します。まず、Q1について、ベース電流IB1とコレクタ電流IC1の関係は、 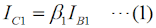 で表されます。コレクタには、ベースに流れる電流のβ倍の電流が流れる、という(バイポーラ)トランジスタの基本の関係です。Q1のエミッタ電流IE1について考えてみると、エミッタ電流はベース電流とコレクタ電流の合計ですから、 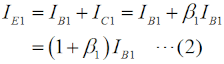 で表されます。一つのトランジスタの解析ならこれで十分ですが、ダーリントン接続では、このQqのエミッタ電流が全てQ2のベース電流になること、つまり、 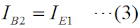 がポイントの一つです。Q1と同様、Q2についても、ベース電流IB2とコレクタ電流IC2の関係を書くと、 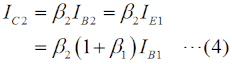 となります。この式の変形では、(2)式と(3)式を使っています。 ここで、Q1とQ2のダーリントン接続を一つのトランジスタと見立てて考えます。まず、そのコレクタ電流ICですが、ICはIC1とIC2の合計ですから、(1)式と(4)式から、 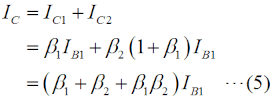 と表せます。ここで、通常のバイポーラトランジスタでは、β1とβ2の大きさが桁違いに違うことはなく、また、1≪β1かつ1≪β2なので、ダーリントン接続を一つのトランジスタと見た時の電流増幅率βは、 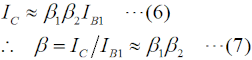 で表せます。Q1が一般的な小信号用トランジスタでβ1≒200、Q2がパワートランジスタでβ2≒50だとしても、β≒β1β2=10000にもなり、非常に大きな電流増幅率が得られることが分かります。 [3]ダーリントン接続の解析 その2…入力インピーダンス次は、入力インピーダンスを考えます。Fig.HD0110_aのモデル(右)を見ると、入力電圧Viは2つのトランジスタのベース抵抗RB1とRB2での電圧降下の和であることが分かります。このことと(2)式から、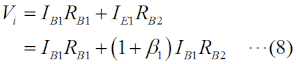 と書けます。入力に電圧Viが掛かっていて、そこに電流IB1が流れているので、入力端子から見たこの回路のインピーダンスZiは、 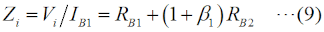 と表せますが、1≪β1なので、(9)式は、 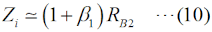 となります。カッコ内の1を無視して、もっと簡単にすれば、Zi≒β1RB2、つまり、入力インピーダンスはおおよそQ2のRB2のβ1倍になる、ということができます。 それでは、解答に移ります。 A…ダーリントン接続を一つのトランジスタと見た時の電流増幅率は、(7)式よりβ1β2です。 B…ダーリントン接続で入力インピーダンスは(10)式より、RB2の(1+β1)倍になります。 C…問題図3の構成であっても、各部を流れる電流の方向は図1と同じです。そう考えれば、このダーリントン接続もNPNトランジスタとして見ることができます。 となります。従って、解答は5と分かります。 入力インピーダンスについては、β1倍ではなくてβ2倍である所に注意すべきですが、パワエレ回路で使う際は、通常、Tr1の方が小信号用でβが大きい物を使うので、入力インピーダンスを大きくしやすいわけです。 この問題の解説はここまでですが、ダーリントン接続が出題された、ということは、同じくトランジスタを複数直接接続したカスコード接続等も出題される可能性がありますので、構造や特徴、用途などを勉強しておいた方が良いと思います。 | |
 |
 |