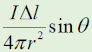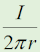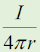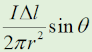アンペールの法則電流磁界の強さ右ネジの法則ビオ・サバールの法則

無線工学 > １アマ > R05年12月期 > A-02
A-02	次の記述は、図１に示すように、0.4 [m]の間隔で平行に置かれた無限長の直線導線Ｘ及びＹに、それぞれ同じ方向の直流電流8 [A]及び10 [A]を流したときの、ＸＹ間の中間点Ｐにおける磁界の強さの値の算出について述べたものである。［　］内に入れるべき字句の正しい組合せを下の番号から選べ。

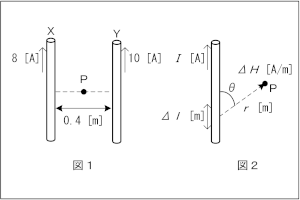
　図２において、導線の微小部分Δｌ [m]を流れる電流Ｉ [A}によって、Δｌからｒ [m]の距離にある点Ｐに生ずる磁界の強さΔＨ [A/m]は、Δｌと点Ｐを結んだ線とのなす角をθとすれば［Ａ］[A/m]の式で求められる。
　一方、ΔＨは導線の微小部分Δｌによるものであるから、これらを導線全体について合成したものが、点Ｐに生ずる磁界の強さＨ [A/m]であり、Ｈ＝［Ｂ］[A/m]で求められる。
　上式より、図１のＸによる点Ｐの磁界の強さＨ_X及びＹによる点Ｐの磁界の強さＨ_Yが求められ、電流の方向からＨ_Xの方向とＨ_Yの方向は互いに［Ｃ］の方向となるので、全体での磁界の強さＨ_Pは、［Ｄ］[A/m]となる。

	Ａ	Ｂ	Ｃ	Ｄ
１			反対	5/π
２			同一	45/π
３			反対	2.5/π
４			同一	22.5/π
５			反対	2.5/π

Fig.H3512A02a

定常電流と磁界の関係を表す法則は、ビオ・サバールの法則とアンペールの法則です。電磁気学の教科書では、これらは「同じ物理現象を違う見方で見たもの」という風に書かれています。この問題はビオ・サバールの方です。　今回（R05年12月期）までは、直線電流１本だけの作る磁界についての問題でしたが、今回は平行に流れる電流２本の作る磁界の合成が出題されました。公式の暗記だけでなく、磁界を「ベクトル」として捉えるようにして下さい。［１］ビオ・サバールの法則は微分形　電流が磁界を作ることは、電磁石などで身近な現象ですが、この関係（電流が磁界を作ること）を定量的に表したものがビオ・サバールの法則と、アンペールの法則です。このうち、ビオ・サバールの法則は、Fig.HA0903_a左のような内容です。
Fig.HA0903_a ビオ・サバールとアンペール	無限に延びる直線状の電流Ⅰの微小長さｄｌがあって、そこから距離ｒの点Ｐに作られる微小磁界ｄＨは、　dＨ＝Ｉdlsinθ/(4πｒ²)　…(1) 　と表されます。θは点Ｐからdlのある部分までを結んだ線と電流がなす角です。　dＨの向きは、電流の向きに進む右ねじを回す向きです。(1)式は、電流上の微小部分の作る磁界です。無限遠に延びる電流のすべての部分が、Ｐ点に影響するのですが、当然、最も近くの位置の影響が大きく、距離の二乗に反比例して弱くなります。
これは、(1)式の分母にｒ²があることでも明らかですが、同時に、直線ですから、遠くなればなるほどθが０やπに近づき、分子のsinθもほとんど０になります。　全ての位置の微小電流の影響を「積分」という演算によって重ねあわせ、計算したものがアンペールの法則です。［２］アンペールの法則は積分形　アンペールの法則は、電流ＩからＲ離れた距離の磁界Ｈが、　Ｈ＝Ｉ/2πＲ　…(2) となるというものですが、これは式(1)をθについてπから０まで積分したものです。具体的な計算は掲載しませんが、電磁気の教科書にはほとんど出ていますので、そちらを参照して下さい。　「無限に長い直線電流なんて存在しないのに、アンペールの法則（(2)式のこと）なんて成り立つのか？」という疑問もあります。確かに厳密には実際の直線電流が作る磁界は(2)式とは違った値になるでしょうが、磁界の強さが電流のある位置からの距離の２乗に反比例するので、無限に長くなくても、そこそこ長ければある精度で近い値になるはずです。それでは解答に移ります。　冒頭でも書いた通り、今回の問題は２本の（無限長の）直線電流が作る磁界の、ベクトル的な合成がテーマです。　Ａ…この選択肢は、(1)式から、[Ｉdl/(4πｒ²)]sinθです。　Ｂ…図２のＰ点に生じる磁界は、(1)式を導線全長に亘って積分したＩ/(2πｒ)です。　Ｃ…電流ＸとＹに垂直で、点Ｐを含む面を（この図の）上から眺めると、電流Ｘによる磁界は（右ねじの法則により）画面の奥向きで、電流Ｙによる磁界は画面に対し手前向きになりますから反対向きです。　Ｄ…図１のＰ点では、２本の無限長電流による磁界（の大きさと向き）を求め、それらをベクトル的に合成する必要があります。　まず、電流ＸがＰ点に作る磁界Ｈ_PXの大きさは、この式（Ｉ/(2πｒ)）にｒ＝0.2 [m]、Ｉ＝8 [A]を代入して、　Ｈ_PX＝8/0.4π＝20/π [A/m] となります。同様に電流Ｙが作る磁界Ｈ_PYの大きさは、　Ｈ_PY＝10/0.4π＝25/π [A/m] となりますが、この問題が問うているのは、両者がＰ点に作る磁界ベクトルの「大きさ」Ｈ_Pなので、　Ｈ_P＝\|Ｈ_PX－Ｈ_PY\|＝\|(20-25)/π\|＝5/π となります。従って、解答は１と分かります。　今回は、電流ＸとＹを含む平面内でＸとＹから等距離にＰ点があったので、磁界のベクトル合成も加減算だけで済みました。ですが、今後、Ｐ点が様々な場所にある問題や、電流の向きが逆、等の様々なバリエーションが出題される可能性がありますので、電界の場合と同様、ベクトルの考え方に慣れ、対処できるようにしておく必要があると思います。

［１］ビオ・サバールの法則は微分形

［２］アンペールの法則は積分形