| □ R05年04月期 A-03 Code:[HB0104] : 抵抗からなる回路網の合成抵抗・枝の電流・未知の抵抗値等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
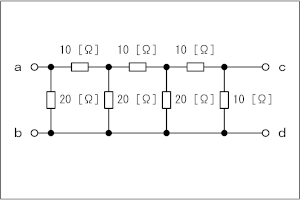
近年、パズルのような抵抗回路の合成が出題されようになりました。これまでに出題されたもの(例えばH3209A03)と似て非なる回路なので、とりあげました。ただ、「あること」に気付けば難しいor計算が面倒な問題ではないと思います。[1]複雑なものは単純化して解くこの手の問題は、上記のH3209A03でも解説しているように、複数の抵抗を合成して行き、単純化して行くことが解法のキーとなります。ただ、この問題は、よく見ると値の特殊性から、割と簡単に答えが出てしまいます。[2]抵抗値をよく見ると回路図を見た瞬間、ご存知の方は「A/D、D/A変換器の内部に使われている、R-2Rラダー回路か」とお気付きになるでしょう。お分かりにならなくても、順に回路を追って行けば難しくありません。 | |
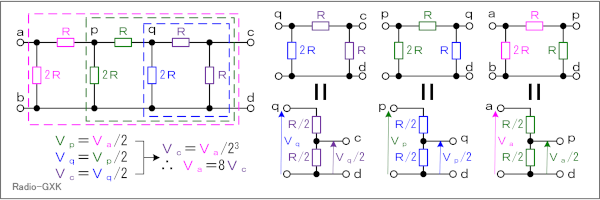 Fig.HB0104_w どう「合成」するか |
|
|
Fig.HB0104_wの左の回路が問題の回路ですが、その中の青の破線枠で示した部分だけを抜出して考えます。なお、この回路の中ほどの2つのノードを、それぞれp、qとし,ノードa−dを基準電位(GND)としておきます。 抜出した回路は同図の右側の3つ並んだ回路の左になりますが、ノードqd間から見た抵抗は2Rと2R(=R+R)の並列なので、Rになります。従って、ノードqに電圧Vqをかけると、ノードcの電圧Vcは Vc=Vq/2 …(1) で表せます。 次に、Fig.HB0104_wの左、緑の破線枠の部分について考えます。ここで、上で求めたように、青の破線枠内の分の合成抵抗はRでしたので、簡単に書けば、同図の右側の3つ並んだ回路の真中になります。これは、その左側の回路と全く同じです。さらに、同図ピンク色の破線枠も同様に緑破線枠内の回路の合成抵抗がRなので、同図の一番右のようになり、ノードpの電圧Vp、ノードaの電圧にはそれぞれ以下の関係が成り立ちます。 Vq=Vp/2 …(2) Vp=Va/2 …(3) ここまでくれば、答えは見通せたようなものですが、(3)式のVpを(2)式に代入し、さらにこの式のVqを(1)式に代入すれば、 Vc=Va/23 …(4) となります。 それでは、解答に移ります。 問題が問うているのは、Vc=3 [V]の時、Vaは何 [V]か、ということですから、(4)式より、 Va=8Vc=24 [V] となるので、3が正解と分かります。 この問題には、抵抗値や電圧違い(今回の問題は、出力電圧から入力電圧を求めるものだが、その逆)、また、ラダーの段数違い等のバリエーションが考えられますが、基本である「次段の入力電圧が前段の入力の一定比率」であることが見抜ければ、後は暗算でも出せるようになります。 | |
 |
 |