| □ H25年12月期 A-19 Code:[HH0802] : 実効長or実効高、電界強度、周波数からアンテナ誘起電圧等を計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| ||||||||||||
| ||||||||||||
この問題を解くには、アンテナの実効長・実効高という概念を理解しておかなければなりません。概念といってもさほど難しいものでもありません。[1]アンテナの実効長・実効高とは何かまず、Fig.HH0802_aを見て下さい。アンテナにはその動作状態で、垂直系のアンテナと、水平系のアンテナがありますが、普通、水平系には「実効長」、垂直系には「実効高」という用語を用います。 | |
|
水平系のアンテナを例に取ると、アンテナに給電すると、そのアンテナの特性で決まる電流分布が生じます。これは、通常一様に分布することはなく、場所によって電流が変化しています。例えば、λ/2ダイポールに中央部から給電すれば、電流は給電部で最も強く、末端に行くに従って正弦的に減少します。 これを、全長に渡って一様な電流が流れている分布、つまりどこを取っても同じ電流が流れている分布だと仮定すると、素子の長さはいくらになるか、という問題です。 |
 Fig.HH0802_a 実効長・実効高の考え方 |
|
Fig.HH0802_a左の図に描いたように、エレメント長の全域にわたってある電流分布をしているアンテナが、全く一定な分布を持っている仮想的なアンテナと同じとすれば、この仮想的なアンテナの全長はいくらになるか、ということです。 垂直系のアンテナに関しても、全く考え方は同じです。アンテナの実際の高さと、電波を送受信するのに、実質的に必要な高さが異なることを言っています。 [2]電界強度と実効長(高)、誘起電圧の関係実効長や実効高を求めて、何の役に立つんだ、と思われるかもしれませんが、実は、ある電界強度の中にこのアンテナを置いた時、アンテナに誘起する電圧が微分も積分も要らず、掛け算だけで出るのです。電界強度の単位は[V/m]なので、実効長[m]または実効高[m]を掛けると、アンテナの誘起電圧 [V]になります。それに、長い(高い)アンテナなのに、実効長/実効高が短い/低いということは、そのアンテナは実際には電波が出ている部分(高周波電流が流れている部分)があまりない、ということが分かります。λ/2ダイポールやλ/4垂直接地といったアンテナの実効長・実効高は、電流分布が単純なので、紙と鉛筆で計算できます(電流分布の導出と微積分が必要なので、証明は行ないません)。λ/2ダイポールの実効長がλ/π [m]で、λ/4垂直接地の実効高がその半分のλ/2π [m]です。 電界強度E [V/m]と、アンテナの誘起電圧V [V]、それにこの実効長Le [m]の関係は、 V=LeE …(1) という、非常に単純な関係です。λ/2ダイポールの場合はL=λ/π、λ/4垂直接地の場合はλ/2πを代入すればよいだけです。 実効長・実効高と似た概念に、アンテナの「実効面積」という考え方があります。これは、空間を流れている受信電波のエネルギーをどれだけ受信機に伝達できるかを面積で表したものです。アンテナと受信機のインピーダンス整合までを考慮に入れた、エネルギー伝達の効率とも呼べるものですが、アマチュアでは出題されたのを見たことがありません。 [3]アンテナに誘起する電圧と受信機入力端に生じる電圧ここで注意して頂きたいのは、上記で求めた電圧Vは、アンテナ単体で、かつ、アンテナ端子が解放の状態での誘起電圧を言っているということです。 | |
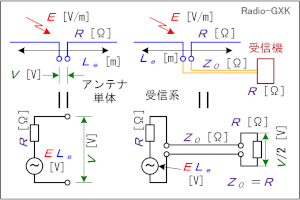 Fig.HH0802_b アンテナ系に生じる電圧 |
アンテナを到来電波の電界中に、単体で置いておいても、受信機なりスペアナなりの機器を繋がなければ、役割を果たしません。 我々が知りたいのは、例えば受信アンテナなら、受信機の入力端子で何[V]得られるのか、ということです。そのためには、アンテナをモデル化してFig.HH0802_bのように考えます。 まずは、アンテナ(放射抵抗R [Ω]、実効長Le [m])が単体で電界E [V/m]中に置かれた場合、同図左のようになります。 これは、(1)式で求めた通り、アンテナ端子に生じる電圧はV=LeE [V]です。この電圧を「受信開放電圧」と呼びます。 |
|
但し、この絵のように、信号源はV=LeEの単なる定電圧源ではなく、信号源抵抗Rを持つ電源にモデル化されていることに注意して下さい。 では、これを受信機(入力インピーダンスR [Ω])に接続したら、入力端で何[V]得られるでしょうか。簡単のため、途中のケーブル等は全てインピーダンス整合が取れていて、かつ、損失はないものとします。 このこと示しているのが、同図右の絵です。ここで証明はしませんが、信号源抵抗を持つ電源の場合、負荷Rが信号源抵抗に等しい時に、最大の電力伝達が可能になります。これは、直流でも高周波でも同じです。厳密に言うと、交流の場合は、一般にインピーダンスZ=R+jXになりますが、信号源抵抗と負荷が複素共役(信号源がR+jXなら、負荷がR−jXの関係)の時に、送れる電力が最大になります。 受信機に入力される「電力」P [W]は、 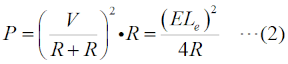 で表せます。また、得られる電圧は、難しい計算をするまでもなく、V/2 [V]です。 アンテナ単体なら得られるはずの電圧の半分しか得られない、というのは何とも残念ですが、信号を伝達する、というのはこういう物理(電圧を上げようとすれば電流が減って電力が減り、電流を増やせば電圧が下がってこれまた電力が減る)なので、高い部品を使っても、納期を掛けても、ベテランを呼んできて設計しても、この値は変わりません。 [4]利得と実効長、実効面積の関係上で、実効面積の話も出ましたが、一般的にアンテナの利得(絶対利得です)がG、放射抵抗がR [Ω]、波長をλ [m]とした時の、これらの関係をまとめておきます。まず、実効長Leについては、(途中の計算は飛ばしますが) 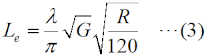 となります。例えば、この式に完全半波長ダイポールのG≒1.64、R≒73 [Ω]を代入してみると、√の項はほぼ1になり、Le=λ/πとなることが分かります。 また、実効面積Aeは 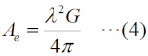 で表せます。 ここで気付くのは、実効面積に放射抵抗が関係ないということです。実効長を求めるには放射抵抗が分かっていなければなりませんが、実効面積は放射抵抗に関係ありません。 それでは、解答に移ります。 これまで出題されていたのは、周波数(=波長)と電界強度が与えられていて、誘起電圧を求めるものでした。この問題は、周波数と誘起電圧から、電界強度を求めるものです。オームの法則を習った時、電圧と電流から抵抗を求めるか、電圧と抵抗から電流を求めるか、という程度の見方を変えた問題で、考え方さえ分かれば難しくありません。但し、従来の問題と同様、「アンテナと受信機入力回路は整合しているものとする」の文言の意味に、十分にご注意下さい。 まず、理想的な(この「理想的な」の意味は、「受信電力が熱に変換されてしまうロスがない」という意味に解して構いません)λ/2ダイポールアンテナの実効長Lはλ/πですから、14 [MHz]では約6.82 [m]となります。 一方、受信機の入力端の電圧Vが96 [mV]なので、すぐに(1)式を変形すれば、求める電界強度Eが出るはずだ…とやると、間違えてしまいます。なぜなら、(1)式のVはあくまでも負荷をつながない時のアンテナ端の誘起電圧であって、整合負荷を接続すれば、電圧は半分になるはずです。つまり、受信機を接続したコネクタの部分で96 [mV]出ているのなら、コネクタを外せば、開放されたアンテナ端では倍の192 [mV]が出るはずです。 つまり、Vに代入すべきなのはこの192 [mV]なのです。後は計算です。(1)をEについて解いて、各値を代入すれば、 E=V/L=192/6.82≒28 [mV] 従って、3が正解と分かります。 「アンテナとマッチングが取れた受信機を繋ぐと、電圧が半分になるのは分かった。じゃぁ、残りの半分はどこへ行ったのか」という疑問が湧きませんか? 実はここからは、1陸技の無線工学Bへの入口です。 アンテナと受信機はマッチング(整合)が取れているので、アンテナに生じた電力は、最大限、受信機に届けられます。ただ、考えてみると、電力を受信機に届けるためには、アンテナにも電流が流れなければなりません。アンテナに電流が流れれば、電波として空間に放射されてしまいます。 つまり、アンテナで受信した電力の半分は受信機に(途中のケーブル等に損失がなければ)ロスなく届きますが、残りの半分は、アンテナから再放射されている、というのが物理的な解釈です。ダイポールだろうが、オフセットカセグレンアンテナだろうが、アンテナの種類や形状には無関係です。受信した電力を半分逃がしている、というのは何とももったいない話ですが、こればかりは物理法則で決まっているので、リンゴが地面から木に「落ち」ない限りは、改善できません。 | |
 |
 |